On the gravitational nature of time

Classical Synchronicity

Let two observers, and agree that should travel between two predefined, arbitrary points in space, and . At place a time keeping device large enough to be observed from . If travels at some agreed upon relativistic velocity, at what time does reach ?

We know the solution to this must be , as demonstrated by the Pound & Rebka experiments along with others that have successfully demonstrated the application of . But how can this be that would observe this time dilation if he is not subject to the same motion as ?

Of course a fundamental piece of the relativistic puzzle is the notion that all motion is only relative, but this is not how it is represented mathematically. Instead, we carve out a special case for gravity, treating the equivalence principle in many ways as being analogous to the motion of space. It is entirely inadequate and nonsensical to claim that an observer who's kinetic state remains unchanged should be subject to the time dilation of .

The only mathematical solution to this fundamental equality, that allows for both classical synchronicity and the application of is that of spatial dilation; time becomes nothing more than a dimensionless, purely mathematical ratio of distances. Of course, the elapsed period between and scales proportionally, but this is purely a secondary effect.

The equivalence principle

As this model proposes the dilation of space with relative motion, we might attempt to ascertain the velocity required to produce our local gravitational parameters. Let us first consider the geometry inherent to our model of cosmic inflation.

If we use the common blueberry muffin analogy, we should first apply a coordinate system to the 'oven'. As our Universe expands into this larger coordinate system, there should be a single point within the two coordinate systems that does not move relative to the other, barring an motion of the universe relative to this larger coordinate system along any of the 3 spatial dimensions. We shall call that point , and presume that all velocities are relative to this position unless otherwise stated.

From this point it is trivial to derive our velocity, first by solving for :

We should then define a so that the integration of this function along our radial vector gives our local gravitational acceleration:

If we first differentiate with respect to :

And then take the average of this integral to obtain a scalar that can be applied in the same manner as :

If we then substitute this value into equation 1, we find:

This gives the cosmological velocity since time itself is not included in the equation at all, giving a velocity that essentially rides the inflation. Since the model being proposed attributes the physical expression of time to gravitational acceleration and cosmic inflation, which become the same process as observed from different reference frames, all cosmic inflation is contained within the velocity when using standard candles at distances approaching the age of the Universe.

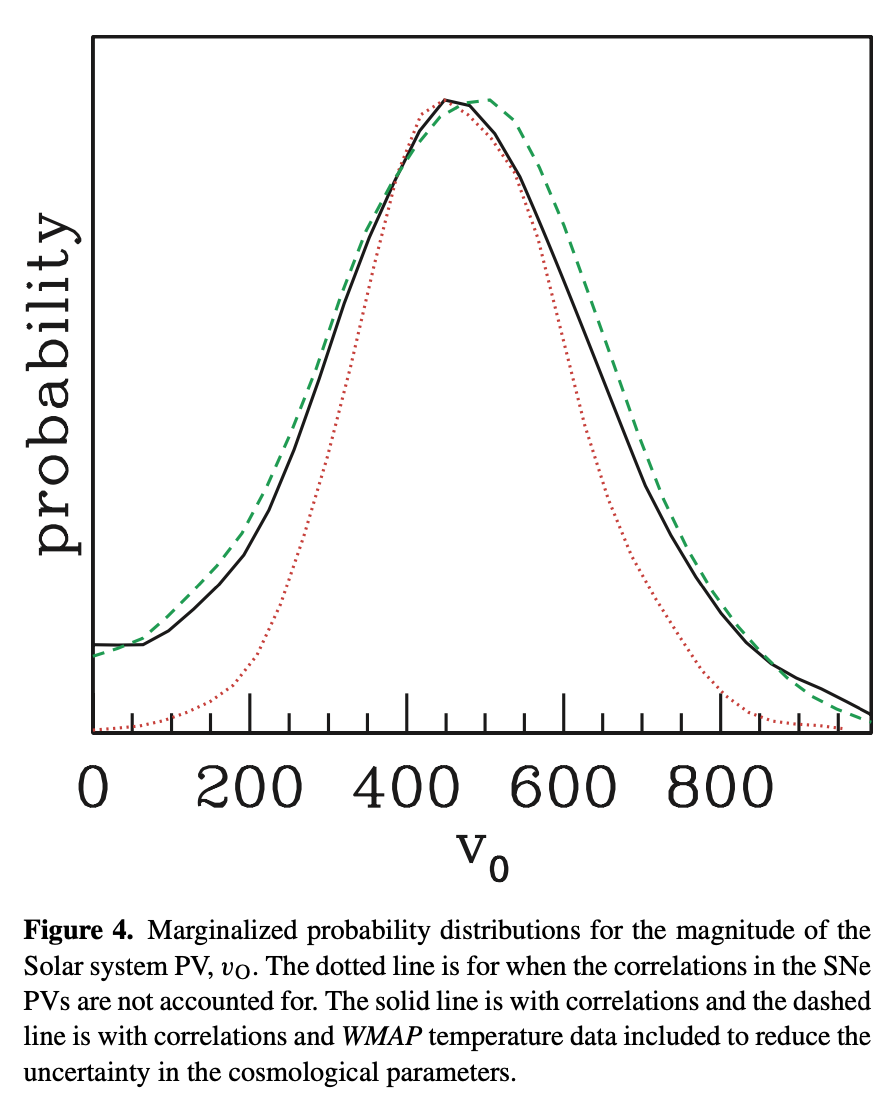
This value coincides closely with the results found by Gordon et el,¹ as well as others that have correlated our velocity relative to the CMB dipole with standard candle observations.

Kinematic Velocity

Let us now consider the role that time plays in this model of relativity. As all of known physics indicates that no 2 bodies can share all 4 coordinates concurrently we must first recognize that time is no longer required to satisfy this property.

As the 4th coordinate commonly attributed to time can now be satisfied by this density axis, time becomes nothing more than a purely mathematical ratio of distances. While this satisfies the property above, we must also reconcile the 4th fundamental derivative. As this dilation of space is a function of motion, we should allow that motion itself occupies this 4th fundamental rate of change.

In a sense, what we've done above is attribute two distinct properties of time to different physical quantities; the driving rate of change as motion, and the temporal coordinate as a position along this density axis.

We can then very simply define a 'time equivalent' quantity as:

We should then define a dilation of space that contains this spatial dilation relative to into account.

By integrating we essentially integrate all of cosmic inflation since the genesis epoch, giving a velocity that is relative to the local coordinate system ie. a purely kinematic velocity.

This value aligns closely with direct observation, falling within 0.5% of measurement in a scenario that would presume a reasonable error due to gravitational turbulence secondary to the same phenomenon applied to other nearby massive bodies.

Time derivative equivalent

Consider that for as it appears in equation , unit of pseudo-time will pass². Because the passage of pseudo-time is defined by the relationship between proportional derivatives and distances, where indicates 1 unit of pseudo-time in units applied to the traditional notion of velocity, we can easily infer the following:

This gives time derivatives per unit of time, but more importantly, a time derivative, that is proportionate to if is defined by .

Kinematic velocity from local orbital parameters

Consider the diagram above, in which a body is in tangential motion with respect to the surface of the Earth. As , we can describe as just . This leaves us with

Expanding this equation gives

Recall from the section above, is equivalent to the number of pseudo-time derivatives in 1 unit of time, proportional to and . In turn, should be equivalent to . of course can be rewritten as the product of the velocity of the gravitational source and the gradient of spatial dilation dilation, .

This then gives

And then simplifying equation the equation above and solving for gives

If we then substitute our standard orbital velocity formula for we find

Discussion

This model satisfies every single experimental confirmation of either SR or GR, and does so without the need to dilate a quantity that we can't directly measure; a quantity that we can't even prove exists as a meaningful physical quantity. By constraining the differences between SR and the model being proposed to such a narrow domain of difference, the model fits incredibly cohesively with established physics. Einstein was insistent on a static Universe early in his career, and because of this missed the obvious conclusion.

This model predicts the lens phenomenon seen in the Bullet Cluster, the lack of gravitational aberration, the Pound-Rebka results and even the following relationship where represents our rotational velocity at the equator.

What is most intriguing however is the relationship this geometry shares with Maxwell's equations. If this model of spatial dilation holds true, , but instead this divergence is equivalent to a determinant determined by the magnitude of our motion as proportional to .

This model draws some bold conclusions, but it is entirely physically and experimentally sound. While the geometry is difficult to wrap ones mind around, it breaks far less pre-relativistic physics than SR & GR themselves.

Footnotes

1. C. Gordon, K. Land, and A. Slosar, “Determining the motion of the Solar system relative to the cosmic microwave background using Type Ia supernovae,” Monthly Notices of the Royal Astronomical Society 387(1), 371–376 (2008). ↩

2. In units of time as they appear in the traditional notion velocity. ↩